OpenCV C++记录(十三)：角点检测算法与亚像素优化

角点是图像的重要特征，往往比边缘和平坦区域具有更独一无二的特征，例如在拼图时，我们往往会先寻找物体对象的角点，最后再完善边缘和平坦区域，对于图像的特征检测亦是如此，角点检测是重要一环。

Harris角点检测

基本原理

1988年，Chris Harris和Mike Stephens提出了角点检测的方法，称为Harris角点检测，其基本思想是考虑窗口到各个方向的灰度差异总和，表示为： $窗口权值函数灰度增量函数灰度函数$

权值函数既可以是普通窗口，也可以是与中心距离相关的高斯窗口。

其中增量项可以根据二元一阶泰勒展开成偏导项Ix和Iy和二阶无穷小：

故原式等于：

此处令M = ，可根据其特征值进一步判断某区域是平坦还是出现边缘还是角点，Harris检测响应公式：

此处的特征值可以理解成两个正交方向的变化率，结论如下：

当|R|很大，为角点，因为此时λ1和λ2均很大，说明两个正交方向都有大的变化率；
当|R|很小，为平坦区，此时λ1和λ2都很小，两个正交方向变化率军均很小；
当R<0, 为边缘，说明λ1和λ2其中一个很小，只有一个方向存在变化率，为边缘；

此处所谓R大还是小的界限由用户确定。

OpenCV实现

OpenCV提供了cv::cornerHarris函数来进行Harris角点检测，主要作用是计算R响应，对于Ix和Iy方向导数，使用了Sobel算子进行计算，对于λ1和λ2，使用了一些线性代数方法来计算特征值，但注意，cv::cornerHarris使用的权值窗口为均值窗口，如果需要高斯窗口可能得自己实现Harris算法，接口如下：

void cornerHarris (
    InputArray src, // 输入图像 (单通道，仅CV_8UC1或者CV_64FC1)
    OutputArray dst, // 输出R响应值CV_32FC1
    int blockSize, // 窗口
    int ksize, // Sobel算子，奇数
    double k, // 矩阵迹倍数k，经验参数取值范围 0.04 ~ 0.06
    int borderType = BORDER_DEFAULT // 边界模式
)

示例:

#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

int main(){
    //图片插值
    Mat rawPic = imread("D:/Documents/Desktop/calib1.png",0);
    // cv::imshow("rawPic",rawPic);

    cv::Mat rRes;
    cv::cornerHarris(rawPic, rRes, 3, 3, 0.04); //滑动窗口大小为3，sobel算子ksize = 3， 系数k=0.04

    cv::normalize(rRes, rRes, 0, 255, cv::NORM_MINMAX, CV_32FC1); //CV_32FC1归一化到0-255像素
    cv::Mat rResC8;
    convertScaleAbs(rRes,rResC8); //转换到八通道数据，以绘制趋势图
    cv::namedWindow("R_Response",cv::WINDOW_NORMAL);
    cv::imshow("R_Response",rResC8);

    cv::cvtColor(rawPic,rawPic, cv::COLOR_GRAY2BGR);
    for(int i=0; i<rawPic.rows; i++){
        for(int j=0; j<rawPic.cols; j++){
            if(rRes.at<float>(i,j) > 254)   //R相应超过阈值，认为可信角点
                rawPic.at<Vec3b>(i,j) = Vec3b(0,0,255);  //标红
        }
    }

    cv::namedWindow("Harris",cv::WINDOW_NORMAL);
    cv::imshow("Harris",rawPic);
    cv::imwrite("D:/Documents/Desktop/Harris.png",rawPic);

    cout<<"Done"<<endl;
    waitKey(0);
    return 0;
}

可见角点被标红： Harris算法

Shi-Tomasi角点检测

基本原理

Shi-Tomasi角点检测于1994年由Jianbo Shi和Carlo Tomasi提出，其基于Harris算法改进而来，仍然基于窗口滑动查找变化率较大的位置，以判断角点是否出现，因此仍然是基于上述的M矩阵判断，但Shi-Tomasi的效果往往优于Harris，其根据变化率阈值来进行角点判断（最小特征值判断），而无需指定k系数，效果比较稳定，其R响应为：

只有当R大于一定阈值，才会判断角点出现。

OpenCV实现

void goodFeaturesToTrack(cv::InputArray image, //输入灰度图C8U1
    cv::OutputArray corners, //输出角点vector
    int maxCorners, //最大检测个数
    double qualityLevel, //一般为0.01到0.1，角点质量
    double minDistance, //最小距离，放置检测点过于密集
    cv::InputArray mask = noArray(), //输入掩图
    int blockSize = 3, //滑动窗口大小
    bool useHarrisDetector = false, //是否使用Harris，false使用Shi-Tomasi算法
    double k = (0.04) //Harris系数，仅前项true才生效
)

示例代码：

#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

int main(){
    Mat rawPic = imread("D:/Documents/Desktop/calib1.png",0);

    std::vector<cv::Point2f> cornersVp;
    cv::goodFeaturesToTrack(rawPic, cornersVp, 20, 0.03, 100, cv::Mat(), 3, false, 0); //检测数量20、质量0.03，最小距离100，滑动窗口为大小3

    cv::Mat drawPic;
    cv::cvtColor(rawPic, drawPic, cv::COLOR_GRAY2BGR);
    for(const auto& pos : cornersVp){
        drawPic.at<Vec3b>(pos.y, pos.x) = Vec3b(0,0,255);  //标红
    }

    cv::namedWindow("Shi-Tomasi",cv::WINDOW_NORMAL);
    cv::imshow("Shi-Tomasi",drawPic);
    cv::imwrite("D:/Documents/Desktop/Shi-Tomasi.png",drawPic);

    cout<<"Done"<<endl;
    waitKey(0);
    return 0;
}

检测顺序与亚像素级检测

对于比较规范的网格图结果，每个角点的响应都是基本一致的情况下，可见角点检测的顺序总是从右下往左上方向检测，即从图像的下到上、从右到左，这点与cv::findContours的寻找逻辑是一样的，体现了OpenCV大量代码采用了这种行优先遍历顺序。

Shi-Tomasi算法的输出是一个cv::Point2f的结果，但并不意味着其是亚像素级别的检测，从打印结果可知所有的检测坐标都是整数，因此其只是为了向后兼容亚像素的精细化，Shi-Tomasi和Harris后如果需要亚像素级精度，可以使用cv::cornerSubPix，这个函数在标定中见过，现在我们来详细叙述其基本原理。

对于Shi-Tomasi算法，因为已经有cv::Point2f数组，直接使用即可：

cv::goodFeaturesToTrack(rawPic, cornersVp, 20, 0.03, 100, cv::Mat(), 3, false, 0);
cv::cornerSubPix(gray, //输入灰度图
                 corners, //输入整数像素坐标、输出亚像素浮点坐标
                 cv::Size(5,5), //优化窗口大小，奇数
                 cv::Size(-1,-1), //死区大小，以优化窗口中心为中心的大小，该死区像素不参与优化
                 //精度和次数迭代 模型，达40次迭代或达0.01精度才退出迭代
                 cv::TermCriteria(cv::TermCriteria::EPS + cv::TermCriteria::MAX_ITER, 40, 0.01)
);

对于Harris算法，需要自己构造一下角点数组再精细化：

cv::Mat rRes;
cv::cornerHarris(rawPic, rRes, 3, 3, 0.04); //滑动窗口大小为3，sobel算子ksize = 3， 系数k=0.04
cv::normalize(rRes, rRes, 0, 255, cv::NORM_MINMAX, CV_32FC1); //CV_32FC1归一化到0-255像素
std::vector<cv::Point2f> vp;
for(int i=0; i<rRes.rows; i++){
    for(int j=0; j<rRes.cols; j++){
        if(rRes.at<float>(i,j) > 254)
            vp.push_back(cv::Point2f(j,i));
    }
}
cv::cornerSubPix(rawPic, vp, cv::Size(5,5), cv::Size(-1,-1), cv::TermCriteria(cv::TermCriteria::EPS + cv::TermCriteria::MAX_ITER, 40, 0.01));

亚像素角点检测数学原理

亚像素角点检测的基本原理是：从亚像素点q到q领域内任一点的向量，都与处的图像梯度正交，即：

其中为在处的图像梯度,，为行向量，为列向量；

需要明晰的是该原理的两个细节，也是算法的目标所在：

假设q为角点的亚像素点，意味其领域点存在两种可能，其一是其存在于内边缘像素的内部或者存在于外边缘像素的内部(图中的)，对于该两种情况，处的梯度都是0，条件成立；其二是其存在于边缘上(图中的)，此时图像梯度垂直于边缘，而为边缘的一个切线，二者正交，内积为0，条件成立；

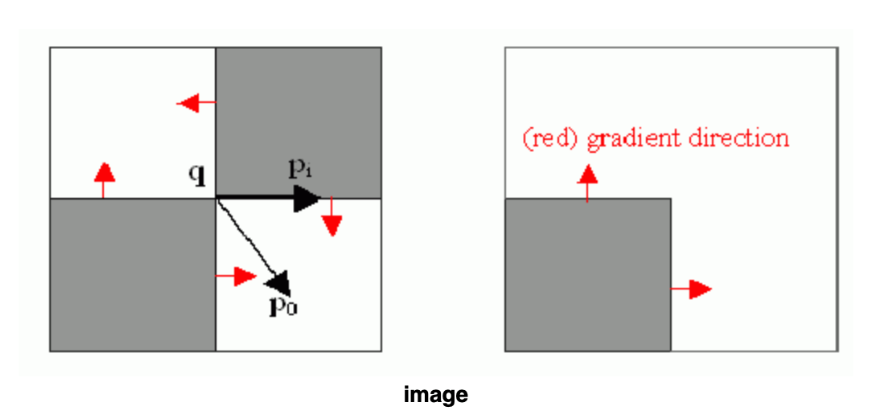两种可能 2. 在实际计算中，亚像素点是多个的联合约束结果，旨在找到点q，该点q与在所有的方向投影量和最小，故与各方向梯度的正交性越强；反过来说，如果q不是边缘亚像素，那么q-p向量在p图像梯度方向的投影就不会取得最小值。

最小二乘法求极值

最小二乘法的目的是求解约束条件最小模长，其中自变量为q的坐标：

令

为了求f(q)的极值，对其求导并令其为0，根据对称矩阵求导法则，若A为对称矩阵，有：

故：

移项得到：

其中：

表示处x和y方向梯度的乘积，其余同理；

这是一个点的情况，当若干个p对q联合约束，而且不同的p距离权重也不同，左右求和得到联合约束方程：

对于右式，其每一项都是确定的，可以看成是常数项，而左侧项则为系数矩阵，这是经典的线性方程组形式：

其解：

其中(二阶矩阵M的逆为主对角线交换、副对角线取反、除以原行列式的值):

至此，就得到了满足或者逼近满足正交性的q的表达式，只要该q的解析式与输入参考点满足一定精度（或者超出估计系统的迭代次数），就认为q为对应的亚像素坐标。

代码实现

了解基本数学原理，OpenCV源码就不难理解了，这里模仿着实现了一份最小二乘法的亚像素优化，其输出和OpenCV接口一致。OpenCV计算中，梯度计算使用了简单的中心差分(f(i+1)-f(i-1))，所以边值需要额外1个像素填充，在计算时只需要从1位置算起，OpenCV使用了data()+偏移量方式代替行遍历以提高性能，完整代码如下：

#include <iostream>
#include <opencv2/opencv.hpp>
#include <assert.h>

using namespace std;
using namespace cv;


void myCornerSubPix(cv::Mat& srcMat, std::vector<cv::Point2f>& corners, cv::Size winSize, cv::Size zeroArea, cv::TermCriteria criterial){
    assert(srcMat.channels() == 1);
    assert((srcMat.rows >= winSize.height*2 + 5) && (srcMat.cols >= winSize.width*2 + 5)); //保证中心差分不发生越界

    const int win_width = winSize.width * 2 + 1;
    const int win_heigth = winSize.height * 2 + 1;

    ///高斯权重窗口
    cv::Mat gaussian(win_heigth, win_width, CV_32FC1);
    float* head = (float*)gaussian.data;
    for(int i=0; i<win_heigth; i++){
        float y = (float)(i - winSize.height)/winSize.height;
        float vy = std::exp(-y*y);
        for(int j = 0; j<win_width; j++){
            float x = (float)(j - winSize.width)/winSize.width;
            head[i*win_width + j] = (float)(std::exp(-x*x) * vy);
        }
    }

    //死区窗口
    if(zeroArea.width >=0 && zeroArea.height >=0 && zeroArea.height < winSize.height && zeroArea.width < winSize.width){
        for(int i=winSize.height - zeroArea.height; i <= winSize.   height + zeroArea.height; i++){
            for(int j=winSize.width - zeroArea.width; j<=winSize.width + zeroArea.width; j++){
                head[i*win_width + j] = 0;
            }
        }
    }

    cv::namedWindow("Gaussian", cv::WINDOW_NORMAL);
    cv::imshow("Gaussian",gaussian);

    cv::Mat subWindows(win_heigth + 2 , win_width + 2, CV_32FC1); //对于中心差分而言，边缘只需要1个像素填充，故扩2

    const int iterNum = (criterial.type & cv::TermCriteria::COUNT) ? std::min(100, std::max(criterial.maxCount,1)) : 100;
    double epsilon = (criterial.type & cv::TermCriteria::EPS) ? std::max(0. , criterial.epsilon) : 0.;
    epsilon *= epsilon; //使用L2范数误差

    for(int num = 0; num < corners.size(); num++){
        cv::Point2f rawPoint = corners.at(num);

        int iter = 0;
        double error = 0;

        cv::Point2f ci = rawPoint;

        do{
            //提取ci为中心的矩形区域，注意Size宽度在前、高度在后
            cv::getRectSubPix(srcMat, cv::Size(win_width+2, win_heigth+2), ci, subWindows, subWindows.type());
            const float* subpix = &subWindows.at<float>(1,1);

            int k = 0;
            //注意，要计算的坐标从1开始，边值只为中心差分
            double sum_wa,sum_wb,sum_wc,bbx,bby;
            sum_wa = sum_wb = sum_wc = bbx = bby = 0;
            for(int i=0; i<win_heigth; i++, subpix += (win_width+2)){ //常量指针，指向可变
                double py = i - winSize.height; 
                for(int j=0; j<win_width; j++){
                    double px = j - winSize.width;

                    float w = head[k];

                    //中心差分梯度
                    double gx = subpix[j+1] - subpix[j-1];
                    double gy = subpix[j+(win_width+2)] - subpix[j-(win_width+2)];

                    double gxx = gx*gx;
                    double gxy = gx*gy;
                    double gyy = gy*gy;

                    //权重累计梯度
                    sum_wa += w * gxx;
                    sum_wb += w * gxy;
                    sum_wc += w * gyy;

                    bbx += w*gxx*px + w*gxy*py;
                    bby += w*gxy*px + w*gyy*py;

                    k++;
                }
            }

            double det = sum_wa*sum_wc - sum_wb*sum_wb;
            if(det <= DBL_EPSILON * DBL_EPSILON) //det远小于double精度，很接近0
                break;

            double scale = 1/det;

            //因为估计量是基于挖出来的图计算的，这里要加上原始中心坐标才是对应原图坐标
            cv::Point2f ci2;
            ci2.x = (float)(ci.x + scale*(sum_wc*bbx - sum_wb*bby));
            ci2.y = (float)(ci.y + scale*(- sum_wb*bbx + sum_wa*bby));

            //L2范数误差
            error = (ci2.x - ci.x)*(ci2.x-ci.x) + (ci2.y - ci.y)*(ci2.y - ci.y); 

            ci = ci2;   //更新坐标

            if( ci.x < 0 || ci.x >= srcMat.cols || ci.y < 0 || ci.y >= srcMat.rows ) //优化的点已经越界
                break;

        }while(++iter < iterNum && error > epsilon);

        //优化点越界，取原值
        if(fabs(ci.x - rawPoint.x) > winSize.width || fabs(ci.y - rawPoint.y) > winSize.height)
            ci = rawPoint;

        corners.at(num) = ci;  //返回亚像素结果
    }

}


int main(){
    Mat rawPic = imread("D:/Documents/Desktop/calib1.png",0);

    std::vector<cv::Point2f> corners;
    cv::goodFeaturesToTrack(rawPic, corners, 5, 0.01, 100, cv::Mat(), 3, false, 0.04); //优化五个角点坐标
    std::vector<cv::Point2f> bak = corners;
    cv::cornerSubPix(rawPic, corners, cv::Size(5,5), cv::Size(-1,-1), cv::TermCriteria(cv::TermCriteria::EPS + cv::TermCriteria::MAX_ITER, 40, 0.01));
    for(const auto& pos : corners){
        cout << "Standard Output: (" << pos.x << "," << pos.y << endl; 
    }

    myCornerSubPix(rawPic, bak, cv::Size(5,5), cv::Size(-1,-1), cv::TermCriteria(cv::TermCriteria::EPS + cv::TermCriteria::MAX_ITER, 40, 0.01));
    for(const auto& pos : bak){
        cout << "My Output: (" << pos.x << "," << pos.y << endl; 
    }

    cout<<"Done"<<endl;
    waitKey(0);
    return 0;
}

结果与OpenCV算法是完全一致的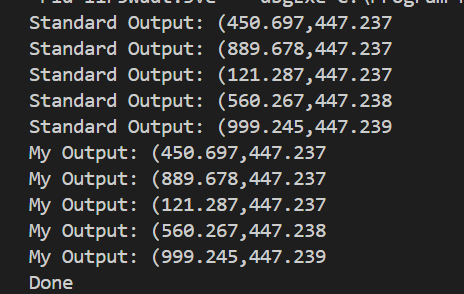：亚像素化结果对比

其中用到接口：

1	cv::getRectSubPix(srcMat, cv::Size(win_width+2, win_heigth+2), ci, subWindows, subWindows.type());

其作用是根据ci中心点截取大小为Size的窗口，如果ci不是整数坐标，会自动按双线性插值计算窗口内的像素。

参考链接：